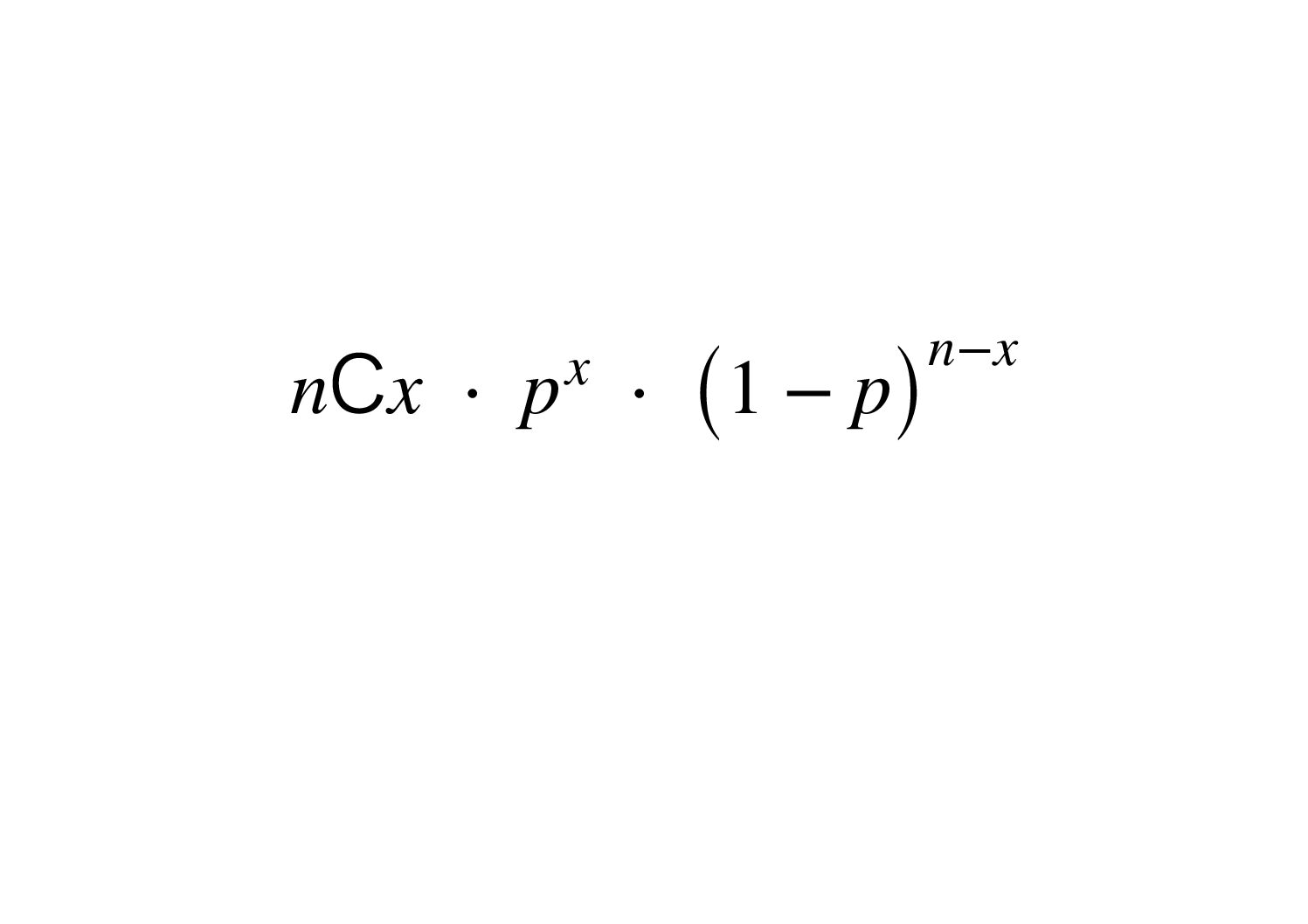前回、二項定理について説明しました
これに関するところとして、数学Aの「場合の数と確率」より反復試行の確率についてお話しします
確率って苦手意識持っている人多いですよねー
状況から計算方法を判断する、すべての状況を見極めるって難しいと思います
だからこそ、練習が必要なんですよね
苦手意識のある人の一助になればと思います
反復試行ってどんな状況？
最初は真面目な言い方をしましょう
ある試行を行うと、確率pで出来事Aが起こるとします
この思考をn回繰り返し行い、出来事Aがx回起きる時の確率を考えたい
こんな時に反復試行の確率を考えます。
（状況例）
コインを１０回投げて、表が３回出る確率を考えたい
サイコロを２０回振って、１が１０回でる確率を考えたい
100分の1の確率で不良品が出てしまう工場で、１万個の製品を作り不良品が10個でおさまる確率を考えたい
くだけた言い方をすると、
同じことを何回も繰り返した時に「こんなとき！」が起こる確率を考えたい
という時に反復試行を使います
「反復試行の確率」考え方と計算
確率が ![\[\frac{1}{10}\]](https://longfeetpenguin-yakitoriteacher.com/wp-content/ql-cache/quicklatex.com-b47d679652d396e3c7d81ad0a9f00b5d_l3.png "Rendered by QuickLaTeX.com")
で「大吉」が出るくじ引きがある
これを５回引いて、３回「大当たり」が出る確率を考えたい
ただし、くじは１度引いたら元に戻すここで１つ、見逃してはいけない部分があります。
同じ条件下で複数回行う試行は、反復試行
「くじを引いたら元に戻す」とありますね
くじを引いたら出てきた「小吉」とか「凶」とか書いてあるものを、２回目を引く前に元に戻すということです
これをやることで、
「１回目で大吉出ちゃったら２回目の人は大吉出にくくなるやん！」
ってことがなくなります
つまりは、１回目も２回目も、５回目も全て同じ条件下でくじを引くことになります
この状態が「同じ条件下で複数回行う試行」ということです
「大吉」と「それ以外」というふうに区別しましょう
反復試行は、YES or NO. の２択です
今回は問題文に「大吉が出る確率」と書いてあるので、「大吉」と「それ以外」という認識をしましょう
こういう関係性を「二律背反」なんて言いますよね
あれこれ詳しく考えたくなる気持ちはわかりますけど、グッと堪えて…
積の法則、和の法則
確率は、要素同士が”and”で繋がっているときはかけ算、”or”で繋がっているときは足し算をします
今回は、「５回中３回大吉が出る」ということですから、
大吉が３回、andで繋がっています
（or だと、1回・２回の２パターンが発生してしまいますね）
同じ理由で、「それ以外」が２回andで繋がっています
さらに、「大吉３回」と「それ以外２回」もandで繋がっています
これらをまとめると、「５回中３回大吉が出て、２回それ以外が出る」という確率は次のようになります
\left( \frac{1}{10} \right)^3×\left(\frac{9}{10}\right)^2起こりやすさを「場合の数」で反映させよう
「５回中３回大吉」は、全パターンの中でどれくらい起こりやすい？
まだ終わらないでください！
「５回中３回大吉が出る」というのはどれくらい起こりやすいのか、まだ式に表していません
そもそも「５回中３回大吉が出る」ってどんな状況なんでしょう？
・最初に大吉を３連続で引いて、あとは「それ以外」をひくパターン？
・１、３、５回目に大吉を引いて、２、４回目に「それ以外」をひくパターン？
いずれも「５回中３回大吉が出る」という状況です
出る順番については問題文は何も言っていませんから、大吉が３回出てくれればそれでいいんでしょうね
これを「出やすさ」とした場合、全部でどれくらいのパターンがあるのでしょう
こういうときは、「枠」を考えるとわかりやすくなります
1番目_____ 、2番目_____、３番目_____、４番目_____、５番目_____
このうち３つに「大吉」が入り、残り２つに「それ以外」が入ります
入れる場所を選べばいいのですから、
_{5}C_{3}通りとなりますね
以上をまとめます
「５回中３回大吉が出る」は、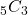
通り起こると考えると
P(くじを５回連続でひき、確率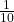
の大吉が３回でる)
![\[ $={_{5}C_{3}}\cdot{\left(\dfrac{1}{10}\right)^3}\cdot{\left(\dfrac{9}{10}\right)^2}$\\ \\ $=\dfrac{5\cdot4\cdot3}{3\cdot2\cdot1}$$\dfrac{1}{10^3}$$\dfrac{81}{10^2}$\\ \\ $=\dfrac{10\cdot1\cdot81}{10^5}$\\ \\ =\dfrac{81}{10000} \\ \]](https://longfeetpenguin-yakitoriteacher.com/wp-content/ql-cache/quicklatex.com-96ffb72925e1dee0f35bf7e264541059_l3.png "Rendered by QuickLaTeX.com")
となります
最後に反復思考の一般系をまとめます
ある試行を１回行うと、確率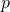
でAという結果が得られるとする。
この試行を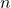
回繰り返し行い、
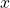回結果Aが得られる確率
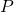は
![\[ P=_{n}C_{x}\cdotp^{x}(1-p)^{(n-x)} \]](https://longfeetpenguin-yakitoriteacher.com/wp-content/ql-cache/quicklatex.com-4b75e17afcf49e5fa0a791b9ea08175a_l3.png "Rendered by QuickLaTeX.com")
と表すことができる。
また、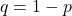
とおくと
![\[ P=_{n}C_{x}\cdotp^{x}q^{(n-x)} \]](https://longfeetpenguin-yakitoriteacher.com/wp-content/ql-cache/quicklatex.com-86109c198677fad7975a65123a7883ee_l3.png "Rendered by QuickLaTeX.com")
と見やすく表現することができる反復試行と二項定理は同じ考え方
反復試行の確率は少しでもわかってもらえたでしょうか
この反復試行の確率の考え方は、二項定理と一緒です
こんな感じです。似てますでしょ？
● 「Aとそれ以外」のように２択であること（このような試行のことを、ベルヌーイ試行といいます）
● 同じ試行を繰り返すこと
この２つの条件に当てはまったら、二項定理や反復試行のような考え方ができる、と理解しておくといいですよ
[おまけ]二項分布(統計)
確率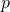で結果Aが起こるベルヌーイ試行を何度も繰り返す状況を考えます
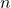回行ったうち、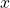回結果Aが起こるときの確率は、二項分布という分布の仕方をします
このとき、二項分布のグラフを表す式は（確率密度関数）
![\[ f(x)=_{n}C_{x}・p^x・(1-p)^{n-x} \]](https://longfeetpenguin-yakitoriteacher.com/wp-content/ql-cache/quicklatex.com-d4134b7737e83cbbc6fbfebce861441f_l3.png "Rendered by QuickLaTeX.com")
平均値
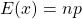分散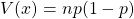
これの詳しい説明は、次の機会にします統計検定を取るべく、私も統計の勉強中です
ブログとか期末試験とかと時期が被っちゃっているのでちょっとスピードが出ていませんが…頑張ります！
それではまた！
Latexできた！！！！！
